Réélections

Je me remets à écrire sur le sujet des élections (et offre un dernier râle à ce blog moribond) à la faveur de la publication, il y a quelques jours, d'un livre de Julia Cagé et Thomas Piketty. Le Monde en a fait un article relativement dithyrambique ici. En complément du livre, Piketty et collègues¹ ont récolté et publié un ensemble de données fascinant : les résultats des élections présidentielles et législatives par communes de 1789 à 2022².

Évidemment, ça me donne l'occasion de revenir sur l'analyse du billet précédent³. Pour rappel, l'idée était d'utiliser le détail du vote des communes pour estimer les flux d'électeurs (ou reports de voix). Le flux d'électeur de X à Y c'est la proportion de Français qui, ayant voté pour X à une élection, votent pour Y à l'élection suivante. Je suis aussi (évidemment) retombé dans le puits sans fond des statistiques associées. Donc ce billet va être composé de 10 % de jolis graphes, de 10 % de socio de café du commerce et de 80 % de stats. En gros la même chose que le billet précédent, mais avec plus de données et (j'espère) des stats un peu plus solides. Pour commencer par les trucs jolis (ici pour le même en pleine page) :

Les traits en gris qui apparaissent lorsque vous survolez le diagramme sont les flux qui ne sont pas significatifs statistiquement. Si vous voulez sauter les trucs chiants et aller voir des jolis graphes, c'est ici.

Douleurs statistiques

If your experiment needs statistics, you ought to have done a better experiment.

-- Ernest Rutherford

Donc, comment obtient-on un flux d'électeurs entre deux années électorales à partir des résultats de chaque commune ? Imaginons qu'une commune ait voté à 100 % pour Mitterrand en 1988, puis qu'en 1995 le vote se soit séparé et que 80 % des électeurs aient voté pour Jospin et 20 % pour Chirac. On en déduit donc que 4/5 des électeurs de Mitterrand ont voté pour Jospin à l'élection suivante et que le reste a voté pour Chirac.

Cette situation hypothétique est évidemment complètement con :

1. Pas beaucoup de communes votent à 100 % pour un candidat. On se retrouve alors avec plus d'inconnues (les flux) que de données (les résultats des élections). Pour s'en tirer, on doit combiner les résultats de plusieurs communes, en supposant qu'elles ont les mêmes flux.
2. Mais ça pose un vrai problème ; les communes ne sont pas toutes identiques et deux électeurs de Mitterrand ne se valent pas. Un bobo parisien et un CGTiste Roubaisien peuvent voter pour le même candidat une année donnée, mais ils représentent évidemment des classes sociales très différentes aux dynamiques de vote qui vont aussi l'être. En langage statistique, les communes ne sont pas identiquement distribuées.
3. Même deux communes parfaitement identiques sociologiquement vont avoir des résultats / des flux différents. Les électeurs votent en partie de manière "aléatoire" : leur contexte géographique, socio-économique et leur historique de vote ne sont pas suffisants pour savoir pour qui ils vont voter (et heureusement).
4. 5 ans, voire 7, entre deux élections présidentielles, c'est long (putain, 5 ans). Suffisamment long pour que des ados deviennent majeurs et commencent à voter et pour que des gens déménagent ou meurent, et donc arrêtent de voter (généralement). Environ 7 % des Français déménagent dans une autre commune chaque année. Environ 1 % meurent. Une partie des flux va donc représenter des remplacements de population⁴ plutôt que des changements d'opinion.
5. Sans même commencer à parler des données manquantes ou erronées : pour beaucoup de communes, on n'a que des données partielles (Toulouse ou Grenoble) et un ensemble de communes appartenant à un département imaginaire (la "Meurthe-et-Moselle") apparaissent presque tous les ans, sauf en 1988⁵.

Avec toutes ces réserves, on peut raisonnablement se dire que toute l'entreprise est à abandonner. Mais bon, on a aussi beaucoup de données (30 000+ communes), alors allons-y quand même.

Malgré mon plus profond désir de faire court et clair, les parties qui suivent ont tout du Methods écrit par un graphomane payé à la lettre. Les stats en elles-même sont aussi usine-à-gaz-esque.

Quantita 'tif

Tout n'est pas perdu, donc. On peut faire les choses bien. Faire des validations croisées, des corrections statistiques, des maths. Pour chaque commune $c$, on cherche une matrice de flux $F_{c, i, j}$ dont la taille dépend du nombre de candidats aux deux élections, et qui vérifie les deux contraintes assez évidentes :

$$ F_{c, i, j} \geq 0 \quad \text{et} \quad \sum_j F_{i, j, c} = 1 $$

Pour trouver cette matrice, on va essayer de minimiser l'expression :

$$ \sum_j \left( \sum_i R^1_{i, c} F_{c, i, j} - R^2_{j, c} \right)^2 $$

Où $R^k_{j, c}$ est la proportion de votants pour le candidat $j$ à l'élection $k$ dans la commune $c$. Comme on ne considère qu'une seule commune, il n'y a pas une solution unique. Si on veut un résultat un peu solide, il va donc falloir regrouper plusieurs communes et minimiser :

$$ \sum_c \sum_j \left( \sum_i R^1_{i, c} F_{c, i, j} - R^2_{j, c} \right)^2 $$

Soit. Mais quelles communes regroupe-t-on exactement ? Considérer la France entière est une très mauvaise idée : des communes différentes n'ont aucune raison d'avoir des matrices de flux identiques⁶. Pour corriger ça, on va vouloir prendre un ensemble de communes relativement similaires à celle qui nous intéresse. Mais des communes similaires vont aussi voter de manière similaire et donc apporter moins d'informations sur la valeur réelle de $F$. Par exemple, dans le cas extrême où les proportions des votes sont exactement identiques, avoir plus d'une commune n'apporte strictement rien. C'est une jolie illustration du dilemme biais-variance, on a le choix entre regrouper beaucoup de communes — augmenter le biais — et faire des regroupements plus petits, de communes très similaires — ce qui rend les valeurs de $F$ moins précises.

Villes jumelles

Bon, c'est bien joli de parler de "communes similaires", mais comment fait-on exactement ? Comme j'ai déjà passé suffisamment de temps sur ce projet, j'ai choisi une méthode assez bourrine. Au sein d'une même région (pré-2015, les nouvelles régions ont des noms à la con⁷), on considère l'ensemble des résultats électoraux et on utilise la méthode des k plus proches voisins. On obtient $K$ communes, qui sont les plus proches, électoralement parlant, de celle que l'on considère.

Pour valider les résultats et regarder à quel point on fait de la merde, on fait une validation croisée. Par exemple, on met de côté la commune originale dans l'algorithme et on regarde à quel point les valeurs de $F$ obtenues permettent de prédire le résultat de la seconde élection à partir de la première. Il y a un optimum à trouver entre précision et biais sur le nombre de voisins ; j'ai fini par choisir $K = 50$ qui avait l'air de ne pas être un trop mauvais compromis⁸.

De toute façon, ces prédictions sont en général de mauvaise qualité : même sur les résultats d'un gros candidat, on va avoir des erreurs qui peuvent aller jusqu'à cinq pour cent des voix. Ce n'est pas si affreux, on travaille avec un modèle avec assez peu de paramètres, et la corrélation est très proche de celle obtenue avec le meilleur modèle linéaire⁹. Cependant, ça met en lumière la limitation principale de ce type de modélisation. Les votes ne sont pas entièrement déterminés par le contexte social-politique-géographique-économique ; parfois, les gens prennent des décisions tout seuls comme des grands. Et parfois, ils votent au hasard. Beaucoup de petits candidats, surtout les "contestataires"¹⁰, sont extrêmement aléatoires. La prédiction d'un modèle linéaire pour Le Pen en 1981 est complètement foireuse, par exemple.

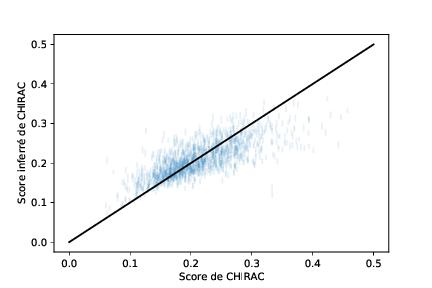
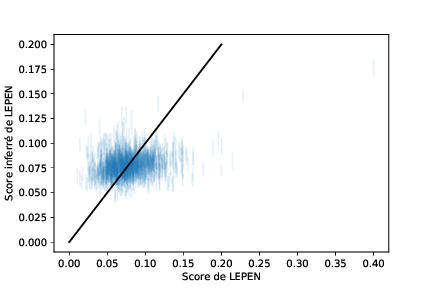
Groupir

Maintenant qu'on a des estimations de flux pour chaque village de France et de Navarre, il reste à regrouper toutes ces estimations. C'est là que les questions comme "qu'est-ce qu'un flux significatif" vont entrer en compte. Intuitivement, on a juste envie de prendre la valeur du flux de chaque commune et de la multiplier par le nombre d'habitants de ladite commune et d'aller faire des choses plus intéressantes de ma vie. Mais c'est un peu bourrin de faire ça directement, parce que les flux ne peuvent pas être négatifs. Donc si l'on observe la distribution d'un flux très faible dans des communes proches, on va observer une distribution qui a un pic en 0 et du bruit autour (en fait, une loi normale tronquée). La moyenne du flux est artificiellement poussée vers le haut par l'impossibilité de définir des flux négatifs. On peut corriger ça assez bien en calculant la moyenne de la loi normale sous-jacente plutôt que la moyenne observée.

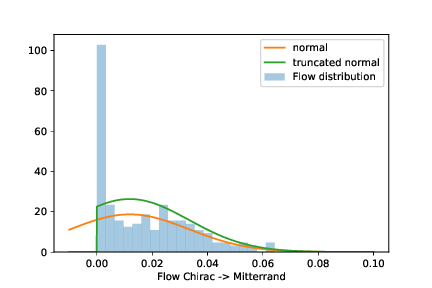
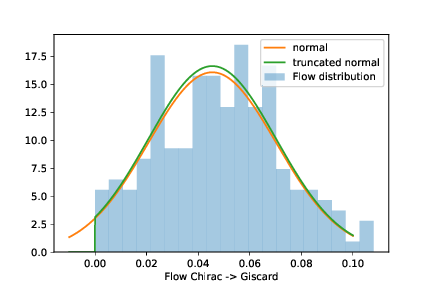
On peut aussi utiliser ces distributions pour estimer quels flux sont "statistiquement significatifs" et lesquels ne le sont pas. On s'enfonce solidement dans le maquis statistique ici, mais l'idée est de dire que si les flux varient beaucoup (en valeur relative) entre deux communes voisines, alors ils ne sont probablement pas représentatifs d'un réel changement d'opinion. L'algorithme aura tendance à "boucher les trous" lorsqu'il ne sait pas, et à inventer des flux fantômes. Par ailleurs, pour les plus petits candidats, on n'a tout simplement pas assez de données solides. J'élimine ces flux supplémentaires a posteriori (un peu arbitrairement, il faut bien dire) : si le coefficient de variation moyen est supérieur à une valeur arbitraire (0.75 ici), alors le flux est considéré comme non significatif.

Un dernier point, à la fin de l'analyse, rien n'impose que la somme des votes doive être conservée, donc ce n'est pas a priori le cas sur le diagramme final (on pourrait le forcer dans une direction ou dans l'autre, mais c'est un peu artificiel).

Sociologie de comptoir

Bon, soyons clairs, ce genre de graphique ne montre pas grand-chose de plus que ce qu'un observateur attentif de la vie politique française sait déjà. Mais ils ont l'avantage d'être jolis (contrairement aux observateurs attentifs de la vie politique française).

Rouge et bleu devant, marron derrière

Une des questions qui a motivé ce billet, c'est la (ré)apparition de l'extrême droite (et particulièrement du FN/RN) en tant que force politique majeure pendant la Ve République. Et le graphique montre des choses intéressantes, je trouve.

Comme je l'avais fait remarquer dans le billet précédent, le parti des Le Pen est étonnamment stable et perd rarement des voix. Zemmour, qu'on présentait souvent comme son fossoyeur, par exemple, ne lui a piqué quasiment aucune voix en 2022. Sarko est le seul homme politique qui a réussi son OPA en récupérant un nombre substantiel de voix du FN en 2007, mais il les a (partiellement) reperdues à l'élection suivante (et a probablement contribué à normaliser le FN par la même occasion, mais j'éditorialise là).

Donc ma question, c'est d'où viennent ces voix. Pour qui votaient les gens qui votent pour le FN maintenant ? On en trouve des traces sur le graphique principal ; à chaque élection pré-2002, il y a des échappées vers le FN depuis Giscard, Mitterrand, Chirac ou Marchais. Mais pour avoir une idée un peu plus précise, on peut regarder l'évolution des votes non pas d'année en année, mais sur une période plus longue, par exemple de 1981 (où le FN était encore négligeable, au point que Le Pen n'avait pas réussi à se qualifier au premier tour) au second tour de 2002 (pays de meeeeerde).

Je ne pense pas qu'il faille attribuer trop de crédit à cette image. 20 ans, c'est une génération, un quart des votants qui se renouvelle, mais on peut quand même dire que le FN ne s'est pas formé sur le dos d'un seul parti (ou groupe politique). Ni de gauche, ni de droite, mais quand même carrément à droite. Ce qui serait amusant à regarder maintenant, c'est ce qui se passe avant '39, à quel point l'électorat de Le Pen est différent de l'électorat de Boulanger ou de Doriot. Potentiellement pour un prochain billet (d'ici 2 ans donc).

De nos jours, le RN est relativement stable, et quand il réussit à récupérer des électeurs au second tour, c'est ceux de la droite (Fillon en 2017 par exemple, voir la section suivante). La "théorie du fer à cheval" est largement fausse de ce point de vue là.

C'est reparti pour un tour

Allez, pour finir comme le billet précédent, voilà tous les flux entre les premiers et seconds tours de 1965 à 2022. Comme ils sont temporellement séparés par seulement deux semaines, beaucoup des problèmes décrits précédemment ne s'appliquent pas et les diagrammes sont particulièrement propres. On peut remarquer :

• 2002 évidemment, où presque tous les Français qui n'avaient pas voté pour Le Pen sont allés mettre leur bulletin pour Chirac (avec St Josse et Mégret en exceptions). Beaucoup de Lepenistes du 1er tour se sont abstenus, par contraste.
• La séparation du vote Le Pen en '88 et '95 en trois parties, une légère majorité qui vote à droite traditionnelle, et le reste qui se sépare en deux entre la gauche et l'abstention (je m'attendais clairement à beaucoup plus d'abstention). Dix ans plus tard, les voix du FN iront largement pour Sarkozy.
• Le partage des voix de Fillon en 2017 et le contraste avec celles de Pécresse en 2022 (certes, il y en avait moins).

---